java.util.Collections 排序原理
版本:JDK7
直接看一下Collections排序中的一个具体实现。
这是sort(List
public static <T extends Comparable<? super T>> void sort(List<T> list) {
// 将list转换成Object数组
Object[] a = list.toArray();
// 调用Arrays.sort 对数组a进行排序
Arrays.sort(a);
// 获取list的迭代器
ListIterator<T> i = list.listIterator();
// 遍历list,将排序之后的数组a里面的元素以此复制到list中
for (int j=0; j<a.length; j++) {
i.next();
i.set((T)a[j]);
}
}
从上面sort方法的声明里面可以看出,要想调用Collections.sort(List
- 容器必须是List的实现类。
- 容器内的元素必须继承或者实现Comparable接口。
Collections中的 sort 方法实际上调用了 Arrays.sort。
下面来看一下Arrays.sort的具体代码实现。
public static void sort(Object[] a) {
// 默认是不启用遗留的归并排序
if (LegacyMergeSort.userRequested)
legacyMergeSort(a);
else
ComparableTimSort.sort(a);
}
LegacyMergeSort 是Arrays的一个静态内部类,只有一个属性 userRequested,默认是 false,所以这里不会去介绍遗留的MergeSort。
static final class LegacyMergeSort {
private static final boolean userRequested =
java.security.AccessController.doPrivileged(
new sun.security.action.GetBooleanAction(
"java.util.Arrays.useLegacyMergeSort")).booleanValue();
}
Arrays.sort内部又调用了 ComparableTimSort.sort 这才是排序的真正实现。
static void sort(Object[] a) {
sort(a, 0, a.length);
}
/**
* @param a, 要排序的数组
* @param lo, 数组的起始下标
* @param hi, 数组的结束下标
*/
static void sort(Object[] a, int lo, int hi) {
// 检查数组:
// 1. 起始下标位置是否大于结束下标位置,如果是,抛出异常。
// 2. 起始下标位置是否小于0,如果是,抛出异常。
// 3. 结束下标位置是否大于数组长度,如果是抛出异常。
rangeCheck(a.length, lo, hi);
// 计算剩余的排序个数
int nRemaining = hi - lo;
// 如果剩余的排序个数小于2,说明数组里面最多只有1个元素,这个时候就不需要进行排序。
if (nRemaining < 2)
return;
// 如果剩余的排序个数,小于32,则进行“mini-TimSort”
if (nRemaining < MIN_MERGE) {
// 获取指定数组中指定位置开始的运行的长度,听起来很绕,先看下面,后面再来看看这个方法具体做什么
int initRunLen = countRunAndMakeAscending(a, lo, hi);
// 进行二分插入排序
binarySort(a, lo, hi, lo + initRunLen);
return;
}
// 当剩余的排序个数大于等于32个的时候,进行TimSort
// ... 后面分析 ...
}
countRunAndMakeAscending
这个方法在ComparableTimSort.sort方法中频繁的出现,它到底是在做什么呢?
/**
* @param a, 待排序的数组
* @param lo, 起始下标
* @param hi, 结束下标
*/
private static int countRunAndMakeAscending(Object[] a, int lo, int hi) {
assert lo < hi;
// 下一个元素的下标
int runHi = lo + 1;
if (runHi == hi)
return 1;
// 下面这个判断主要是为了返回最后比较的下标位置,并且将runHi前面比较的元素以升序的方式排列起来。
// 如果是倒序,那么翻转数组
if (((Comparable) a[runHi++]).compareTo(a[lo]) < 0) {
// 倒序
while (runHi < hi && ((Comparable) a[runHi]).compareTo(a[runHi - 1]) < 0)
runHi++;
// 翻转数组
reverseRange(a, lo, runHi);
} else { // 升序
while (runHi < hi && ((Comparable) a[runHi]).compareTo(a[runHi - 1]) >= 0)
runHi++;
}
// 返回初始位置到最后一个被比较的元素的距离
return runHi - lo;
}
// 这个方法很简单,就是对指定数组内的某一块连续元素进行位置倒序。
private static void reverseRange(Object[] a, int lo, int hi) {
hi--;
while (lo < hi) {
Object t = a[lo];
a[lo++] = a[hi];
a[hi--] = t;
}
}
countRunAndMakeAscending 这个方法就是做了 2 件事情:
-
count RUN,顾名思义就是记录运行次数,其实也就是记录了当前数组 compare 到哪里的数组下标位置,方法结束将下标位置 返回。
-
make ascending,将数组从 lo 到 runHi 之间的所有元素,按照升序排列。
ComparableTimSort.sort 里面涉及了两种排序:
- binarySort,其实是一种二分插入排序。
- TimSort,是结合了合并排序(merge sort)和插入排序(insertion sort)而得出的排序算法。
BinarySort
原理
算法的基本过程:
-
计算 0 ~ i-1 的中间点,用 i 索引处的元素与中间值进行比较,如果 i 索引处的元素大,说明要插入的这个元素应该在中间值和刚加入i索引之间,反之,就是在刚开始的位置 到中间值的位置,这样很简单的完成了折半。
-
在相应的半个范围里面找插入的位置时,不断的用(1)步骤缩小范围,不停的折半,范围依次缩小为 1/2,1/4,1/8 …….快速的确定出第 i 个元素要插在什么地方。
-
确定位置之后,将整个序列后移,并将元素插入到相应位置。
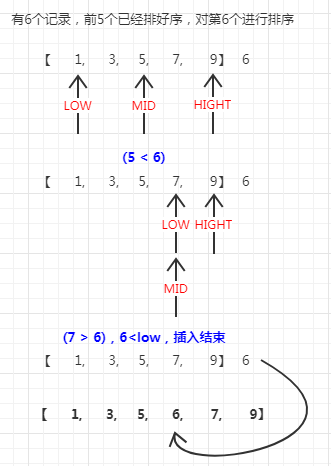
了解二分法插入排序原理之后,来看一下 ComparableTimSort 中的具体实现。
/**
* @param a, 待排序的数组
* @param lo, 起始下标
* @param hi, 结束下标
* @param start, 开始a[start]以后的数组都是未排序的元素,需要通过二分法插入
*/
private static void binarySort(Object[] a, int lo, int hi, int start) {
assert lo <= start && start <= hi;
if (start == lo)
start++;
// 循环遍历a[start]以及a[start]以后的所有元素,按照二分插入的规则有序的插入数组中
for ( ; start < hi; start++) {
@SuppressWarnings("unchecked")
Comparable<Object> pivot = (Comparable) a[start];
// 设置有序的范围,left是有序数组开始的位置,right是有序数组结束的位置
int left = lo;
int right = start;
assert left <= right;
// 这个while循环就是要找到插入点
while (left < right) {
// mid为(left+right) / 2
int mid = (left + right) >>> 1;
if (pivot.compareTo(a[mid]) < 0)
right = mid;
else
left = mid + 1;
}
assert left == right;
/*
* 上面找到的插入点,必然满足下面两个条件:
* 1. a[start] 大于等于所有在[lo, left)范围内的元素
* 2. a[start] 要小于所有在 [left,start)范围内的元素
*/
int n = start - left;
// 进行插入操作
switch (n) {
case 2: a[left + 2] = a[left + 1];
case 1: a[left + 1] = a[left];
break;
default: System.arraycopy(a, left, a, left + 1, n);
}
a[left] = pivot;
}
}
TimSort
TimSort 算法为了减少对升序部分的回溯和对降序部分的性能倒退,将输入按其升序和降序特点进行了分区。排序的输入的单位不是一个个单独的数字,而是一个个的块-分区。其中每一个分区叫一个 run 。针对这些 run 序列,每次拿一个 run 出来按规则进行合并。每次合并会将两个 run合并成一个 run。合并的结果保存到栈中。合并直到消耗掉所有的 run,这时将栈上剩余的 run合并到只剩一个 run 为止。这时这个仅剩的 run 便是排好序的结果。
Timsort的核心过程
-
如果数组长度小于某个值,直接用二分插入排序算法
-
找到各个run,并入栈
-
按规则合并run
ComparableTimSort的初始化
在讲 TimSort 之前先了解一下ComparableTimSort的初始化。
private ComparableTimSort(Object[] a) {
this.a = a;
int len = a.length;
@SuppressWarnings({"unchecked", "UnnecessaryLocalVariable"})
// 根据待排序的数组的长度创建一个临时数组
// 若待排序的数组长度小于512,临时数组长度为待排序数组的1/2
// 否则临时数组为256
Object[] newArray = new Object[len < 2 * INITIAL_TMP_STORAGE_LENGTH ?
len >>> 1 :
INITIAL_TMP_STORAGE_LENGTH];
tmp = newArray;
int stackLen = (len < 120 ? 5 :
len < 1542 ? 10 :
len < 119151 ? 24 : 40);
runBase = new int[stackLen];
runLen = new int[stackLen];
}
下面来看一下 ComparableTimSort 中的实现,下面这段是继上面 ComparableTimSort.sort(Object[] a, int lo, int hi) 的代码。
ComparableTimSort ts = new ComparableTimSort(a);
/**
* 获取minRun,之后待排序数组将被分成以minRun大小为区块的若干个子数组。
* 1. 如果nRemaining大小为2的N次幂,则返回16(MIN_MERGE / 2)
* 2. 其他情况下,逐位向右位移(即除以2),直到找到介于16和32间的一个数
*/
int minRun = minRunLength(nRemaining);
do {
// 在a[lo]到a[runLen-1]是按照升序排好的数组
int runLen = countRunAndMakeAscending(a, lo, hi);
// 如果剩余未排序的数组长度小于minRun的长度,那么就不需要归并排序,直接采用二分法插入排序即可
if (runLen < minRun) {
// nRemaining 和 minRun中取最小
int force = nRemaining <= minRun ? nRemaining : minRun;
// 二分插入排序
binarySort(a, lo, lo + force, lo + runLen);
// 更新已经被排序的元素长度
runLen = force;
}
// 记录当前已经排序的各区块的大小
ts.pushRun(lo, runLen);
// 进行归并插入
ts.mergeCollapse();
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0); // 直到所有元素被排序,结束循环
assert lo == hi;
// 若此时还有未合并的区块,就强行合并。
ts.mergeForceCollapse();
assert ts.stackSize == 1;